Sobre

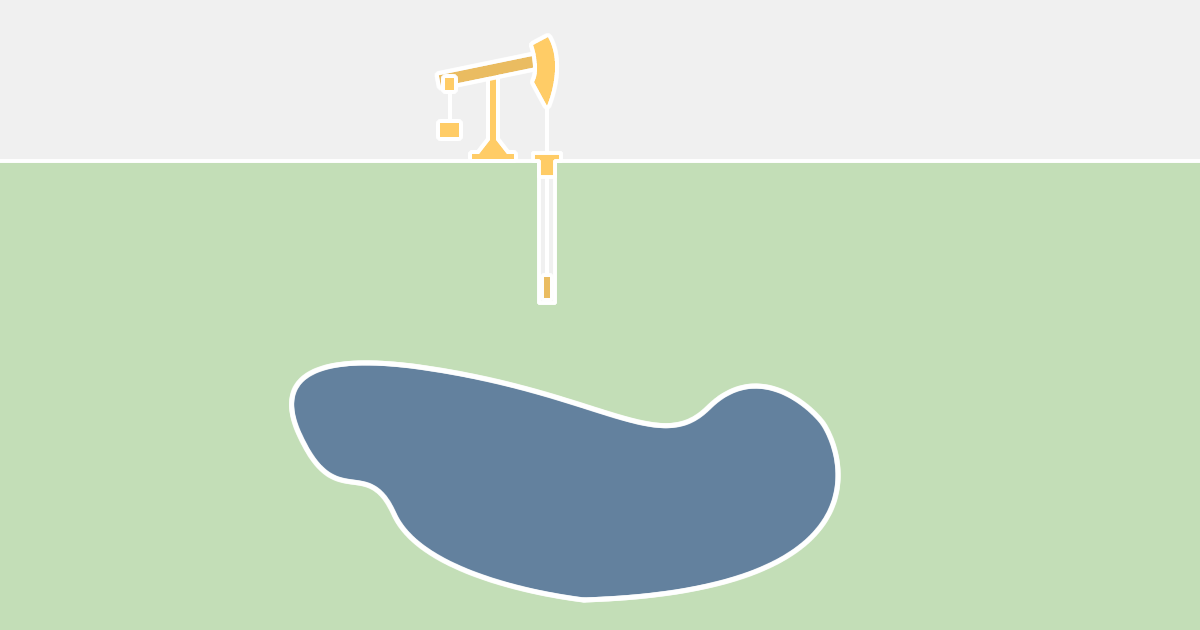
Imagine que uma petrolífera descobriu um poço, já fez uma análise geológica do local e obteve um mapa do poço, mas também descobriu que a estrutura em volta do poço é fraca e pode ceder se for aplicada muita pressão. A extração consiste em furar da superfície até o poço com uma broca, mas a broca produz muito calor ao atritar com a terra e esse calor pode aumentar a pressão que o petróleo exerce sobre a estrutura do poço inviabilizando a operação. Tendo em vista a análise dos geólogos, vale que a temperatura média máxima que o petróleo pode atingir é de 400K. Como explorar o poço sem ultrapassar essa limitação? a broca pode funcionar constantemente por todo tempo? deve funcionar ligando e desligando de 10 em 10 minutos? de 5 em 5 minutos?

Provavelmente um aluno de Matemática computacional nunca vai ter estudado nada sobre poços de petróleo, brocas ou como obter informações geológicas. E isso não é um problema. Conseguimos começar a rascunhar o problema mesmo assim.

Sabemos a temperatura de cada ponto do poço dos arredores antes da influência da broca e também sabemos a temperatura na qual a broca se mantém ao funcionar. Precisamos saber como a temperatura da broca influencia no resto do ambiente. Numa pesquisa no Google ou em alguma matéria da física sobre termodinâmica esbarramos na equação do calor:

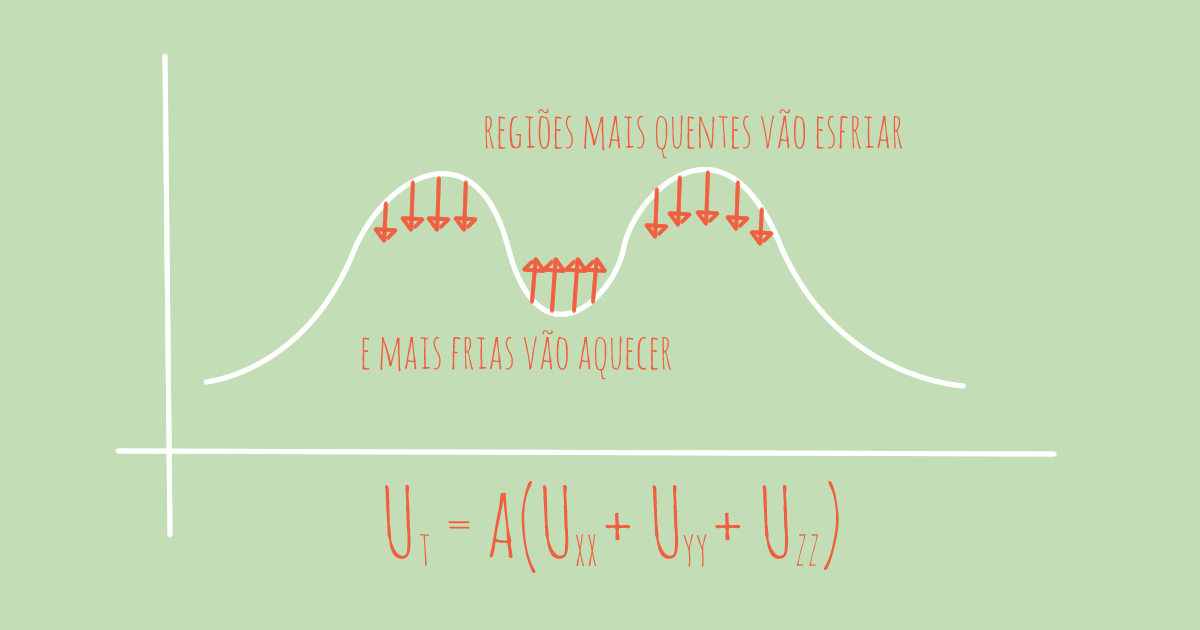
Buscar uma solução dessa equação é encontrar uma função U(x,y,z,t) que satisfaz a equação. Ou seja, encontrar as temperaturas do poço e proximidades em todos os tempos do nosso interesse.

Aprendemos em matérias sobre equações diferenciais que esse tipo de equação possui inúmeras soluções possíveis, mas que ao fixarmos o valor da função no tempo inicial (ou seja, se soubermos as temperaturas iniciais em cada ponto) e fixarmos também os valores da função na fronteira (ou seja, se conseguirmos delimitar o domínio da função e nos pontos de fronteira informar a temperatura em todos os tempos) é possível obter uma solução única. Essas condições são ditas condições de valor inicial e de contorno. É essa solução que estamos buscando.

Normalmente sabemos qual é o valor da função no tempo inicial, já que antes da aproximação da broca basta utilizar a temperatura que os geólogos fornecem. O mesmo vale pra temperatura que obtemos em pontos distantes da ação da broca, onde podemos fixar nossa fronteira. Perceba também que de tempos em tempos a própria fronteira está mudando, afinal a broca vai perfurando a terra e o ponto de entrada de calor no sistema muda de lugar.

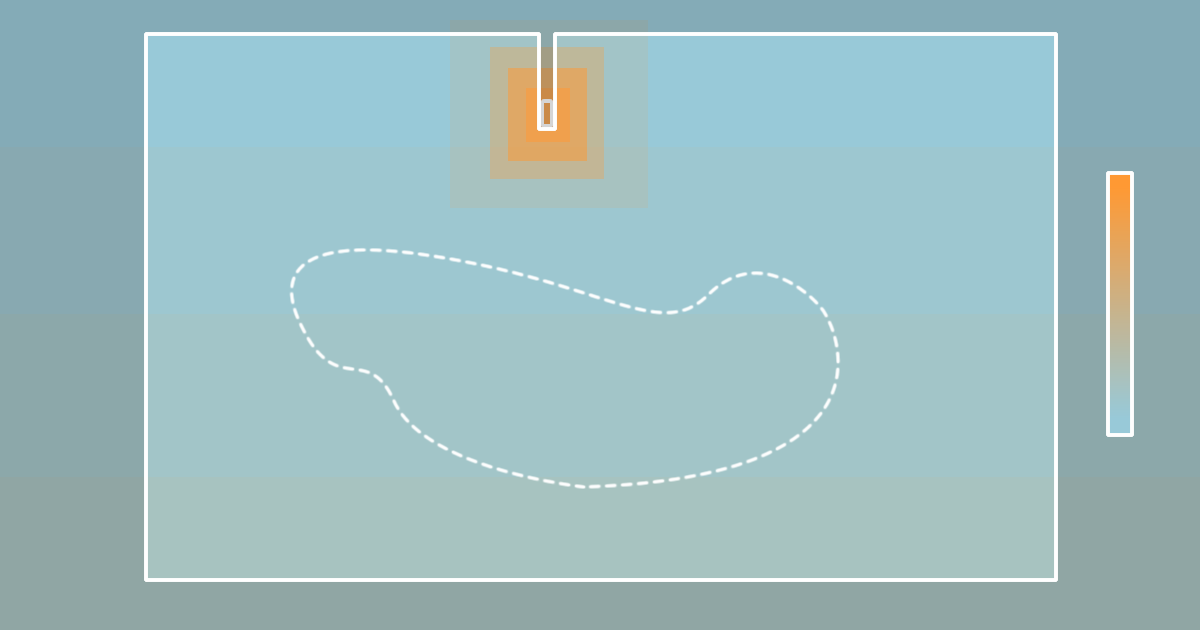
Agora a matemática nos diz que existe uma única solução, mas não aponta qual é a solução.

Quando o domínio sobre o qual estamos estudando a equação do calor é suficientemente comportado, como quando é um círculo ou um retângulo e tem condições iniciais e de contorno bem comportadas — contorno valendo zero, por exemplo — é fácil obter, manipulando símbolos e com o auxílio de alguns teoremas a solução, exata da equação, ou seja, conseguimos obter os valores de U(x,y,z,t) com perfeição em qualquer ponto do domínio. Esse tipo de solução é chamada solução analítica.

Nem sempre parece possível encontrar uma solução analítica. Precisamos então buscar uma solução numérica, que consiste de uma aproximação da solução analítica — sim, é possível aproximar uma função sem sequer conhecer essa função. A solução numérica, antes de tudo, restringe um pouco o domínio: agora não vamos buscar mais os valores em todos os pontos (x,y,z) e em todos os tempos. Vamos buscar apenas nos pontos do tipo x = 1m, 2m, 3m, …, y = 1m, 2m, 3m, …, z = 1m, 2m, 3m, …, e t = 0, 1s, 2s, 3s. Ou seja, vamos discretizar o domínio. Assim para saber a temperatura no tempo 1.8s na posição (0.3, 0.8, 1.9) vamos olhar pro tempo 2s na posição (0,1,2) e entender que aquilo é uma aproximação. Claro que não precisamos aproximar de metro em metro e segundo em segundo, pode ser a cada 10 centímetros ou a cada 34 milímetros, quanto mais fina é a malha criada melhor esperamos que seja a aproximação.

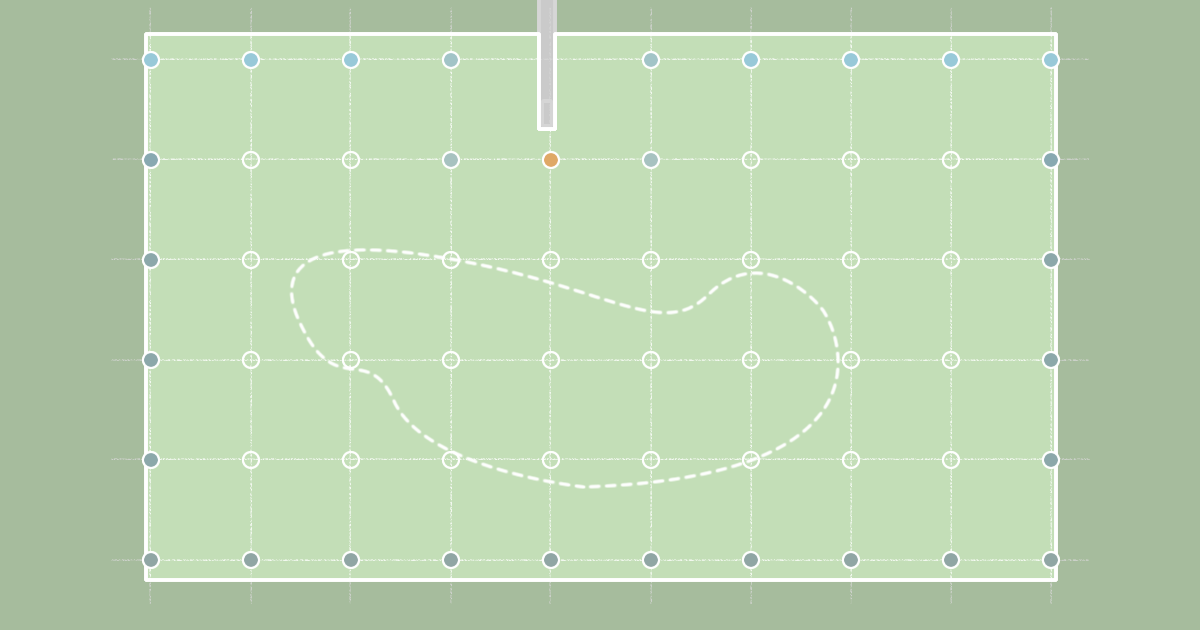
Agora que restringimos nosso domínio fazendo dele uma malha precisamos entender como aplicar a equação do calor nesse novo domínio.

Os elementos presentes na equação do calor são derivadas (U_t, U_xx, U_yy, U_zz) e esses objetos matemáticos só são bem definidos em um ponto quando é possível sempre achar pontos cada vez mais próximos desse ponto. Mas tomando um ponto qualquer na malha é sempre possível isolá-lo…, ao contrário do domínio inicial onde nenhum ponto pode ser isolado.

Existe então o problema de transformar a equação que precisamos resolver em algo possível de aceitar uma solução numérica. Em Equações Diferenciais Numéricas estudamos como fazer isso, aqui vamos usar um método conhecido por Crank-Nicolson.

Esses métodos numéricos trabalham da seguinte forma: dado um tempo eles calculam o próximo tempo usando os valores do tempo anterior. Assim, para saber o que aconteceu no tempo 500s é preciso calcular desde o tempo 1s até o tempo 500s.

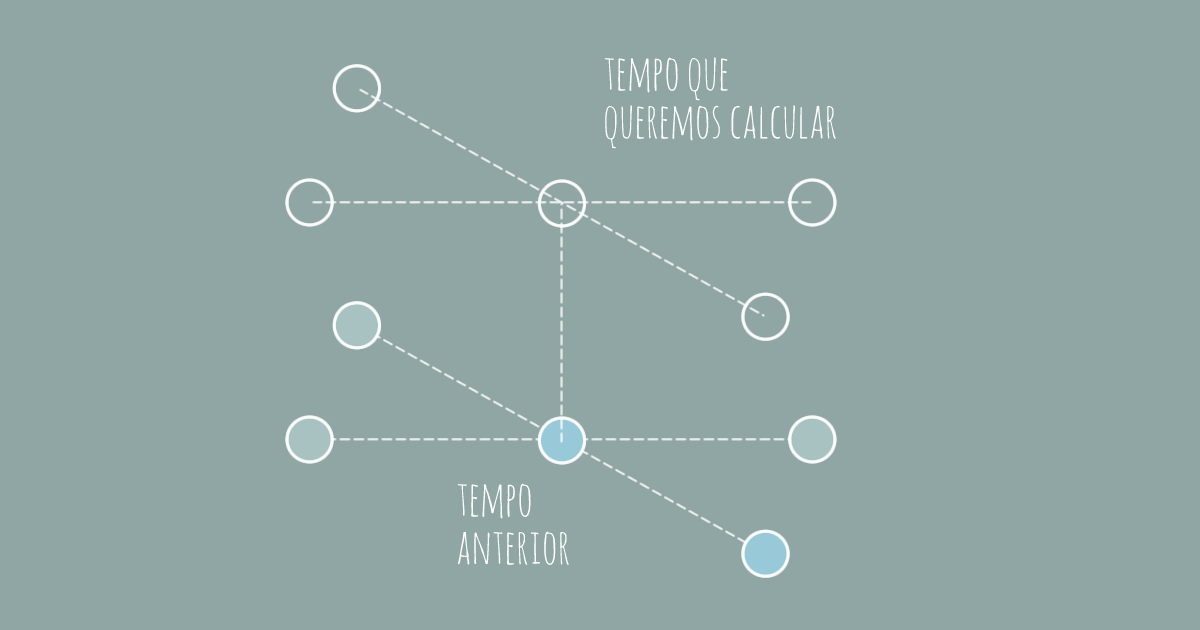
Para calcular o valor num ponto (x,y,z,t) o CN faz uso de alguns pontos abaixo desse no tempo anterior e também de pontos do tempo atual. Como os pontos do tempo atual só são conhecidos quando estão na fronteira isso acaba produzindo relações entre os pontos que culminam num sistema linear!

Esse sistema produzido, dependendo de quão fina é a malha escolhida, pode ter centenas, milhares ou milhões de linhas. É humanamente impossível resolver algo assim na mão.

computadores são capazes de trabalhar com objetos discretos e finitos, como o conjunto de pontos da malha em cada tempo. Para resolver o CN precisamos de informar para o computador, passo a passo, como obter o sistema linear e como resolvê-lo e para resolver rápido esse sistema linear podemos novamente recorrer a matemática e estudar propriedades específicas desse sistema linear — no caso do CN a matrix é tridiagonal e com isso é possível escrever algoritmos que o resolvem muito mais rápido. Aqui vemos a tal ponte trabalhando nos dois sentidos: estamos usando um computador pra resolver um modelo matemático e ao mesmo tempo usando a matemática pra fazer com que o computador resolva isso mais rápido.

Existem outros problemas que surgem ao tentar resolver esse sistema linear: qual é a melhor forma de representar ele no computador? e se não couber na memória? Aprendemos métodos de avaliar e responder essas perguntas em matérias como Algoritmos e Estruturas de Dados e em Álgebra Linear Numérica.

Resolvidos esses problemas já conseguimos simular o funcionamento da broca.

Mas calma… nós não resolvemos o problema da vida real, e também não resolvemos o modelo matemático por completo (equação do calor), resolvemos apenas uma aproximação: como garantir que nossa aproximação é boa o bastante pra justificar que não vamos perder uma broca que a empresa levou anos pra desenvolver?

Retornamos à matemática, usando propriedades que são estudadas em Análise I e II, conseguimos obter uma margem de erro que relaciona o quão próxima nossa solução da solução exata. Se, considerando o erro, nossa simulação ainda estiver dentro do aceitável tudo bem, caso contrário, se ela passar por pouco do aceitável pode ser interessante refinar mais a simulação para reduzir o erro e ter certeza.

Legal o exemplo, mas e o curso, ele é sobre…

Se tornar capaz de resolver esse tipo de coisa sozinho, mesmo que com um bocado de trabalho.

Embora as matérias do curso sejam abstratas e não trabalhem diretamente com exemplos como esse, no final das contas os formados, que geralmente sentem que sabem muito sobre coisas isoladas, quando confrontados com problemas no mercado acabam percebendo que conseguem juntar as peças necessárias e que são capazes de absorver o conteúdo específico necessário para aquele trabalho sem muito problema.

No correr do texto também deve ter ficado claro que a matemática que vemos no curso é distante da matemática do ensino médio. Aqui estamos preocupados em entender e definir como algumas ideias e propriedades conseguem implicar outras propriedades, estudar padrões — não padrões numéricos ou fractais em imagens, mas conseguir maneiras de dizer que sempre que vemos um conjunto de propriedades podemos ter certeza que também haverá uma outra.

Nessa matemática — e também na computação — , muitas vezes estudamos ideias que não parecem possuir muita relação com o mundo real, nem sequer foram feitas com o intuito de modelar ou falar algo sobre o universo, mas apenas pra cumprir algum capricho estético. E mesmo nesses casos as consequências dessas ideias acabam produzindo ferramentas úteis e estimulando a criatividade na produção de modelos e soluções.